Algofejtörők alkalmazhatósága az algoritmikus gondolkodás fejlesztése érdekében

Burai Gyöngyi

burai.gyongyi@tok.elte.hu

Absztrakt: A cikk az algoritmikus gondolkodás fejlesztésének egy lehetséges eszközére, az algofejtörő feladatokra irányuló kutatás 2009-ben született tapasztalatainak egy részét kívánja bemutatni. Az algoritmikus gondolkodás és az algofejtörő fogalmának kifejtése után általános iskola második és negyedik osztályában lezajlott megfigyeléseket és az ezekből nyert következtetéseket írja le. A megfigyelés tárgya különböző típusú és különféle eszközökkel támogatott algofejtörők megoldatása a tanulókkal.

Bevezetés

Mindennapi életünk szerves részeként alakítunk ki tudatosan vagy tudattalanul olyan ismétlődő eljárásokat, melyeket meghatározott sorrendben, lépésenként hajtunk végre. Az esetek nagy részében észre sem vesszük, de gyakorlatilag algoritmizációt végzünk. Ez a cselekvés nem csak arra alkalmas, hogy rendszert és felépítést vigyen hétköznapi tevékenységeinkbe, hanem általa energiát és időt is megtakarítunk. Az algoritmikus gondolkodás kialakulása egyértelműen a gyermekkorhoz köthető, legfontosabb időszaka az óvoda és az általános iskola által keretezett időszakra esik. Éppen ezért célszerű és elengedhetetlen ebben az időszakban a képesség fejlesztése célzott módszertan segítségével.

Az algoritmikus gondolkodás messze túlmutat magán az informatikán. Sajnos az iskolai oktatás egyre inkább eltolódik az alkalmazói rendszerek használata felé, így egyre jobban elhanyagolják ennek az igen fontos képességnek a fejlesztését. Bár a NAT-ban visszatérő irányadás a gyermekek algoritmikus gondolkodásának fejlesztése, nem létezik jelenleg Magyarországon olyan általánosan elfogadott és bizonyított hatékonyságú pedagógiai eszközrendszer, mellyel akár informatika órán, akár bármelyik másik tanórán a NAT által elvárt eredmény biztosítható.

Az algofejtörők története

Az elnevezés a kanadai matematikus, számítógép-tudós és filozófus A. K. Dewdney-től származik, aki számos könyvet írt a modern számítástechnika jövőjéről és hatásairól. Algofejtörő feladványaival a Tudomány (Scientific American) című folyóirat általa szerkesztett Számítógépes észjáték című rovatában találkozhatunk.

„Vannak azonban olyan fejtörők is, ezeket algofejtörőknek nevezem, amelyeknek bonyolultabb a megoldásuk: egy, a kívánt végállapotot előállító „recept” vagy eljárás, más szóval algoritmus.”[1]

A hagyományos fejtörő irodalomban is találkozhatunk algofejtörő feladványokkal. Például, amikor a révésznek kell átjuttatnia a folyó túlsó partjára egy farkast, egy kecsét, és egy káposztát, vagy amikor egy kétkarú mérleg segítségével kell kiválasztanunk a hamis golyót, ami csak súlyában tér el a többitől.

Ezen feladatok érdekességének és újszerűségének köszönhetően motiváló hatásúak, ösztönzik a tanulókat a probléma megoldására, a közös okoskodásra, az erőfeszítésre a siker érdekében. Segítségükkel átalakíthatjuk a tanulók gondolkodásmódját, nagyobb teret biztosíthatunk a kreatív gondolkodás számára, fejleszthetjük a probléma felismerésének képességét.

Az algoritmikus gondolkodásról

A gondolkodás szerepet játszik minden olyan szellemi tevékenységben, melynek célja valamilyen probléma megfogalmazása vagy a probléma megoldásának megtalálása. Az algoritmikus gondolkodás lényege, hogy a tanulók ne műveletekben, hanem műveletek folyamatában, eljárásokban gondolkozzanak. Az algoritmikus gondolkodás négy szintre bontható, és mindegyik szint szoros kapcsolatban áll a különböző gondolkodásmódokkal.

Az algoritmikus gondolkodás négy szintje[2]:

1.       Már ismert algoritmus alkalmazása adott problémára

Deduktív gondolkodás: egy általános és igaznak feltételezett tételből kiindulva lépésről lépésre levezetünk egy résztételt

2.       Algoritmus megalkotása: a tanuló a problémamegoldás során felismeri a szabályszerűséget, ezt értelmes formában rögzíti

Induktív gondolkodás: az egyedi esetekből kiindulva következtetünk az általánosra

3.       Algoritmusok felkutatására irányuló tudatos törekvés: hasonló probléma esetén a már ismert algoritmust kissé módosított formában alkalmazza

Analogikus gondolkodás: két vagy több adatnak, jelenségnek bizonyos tulajdonságokban való egyezéséből, vagy hasonlóságából más tulajdonságokban, struktúrákban való egyezésre, vagy hasonlóságra következtetünk

4.       Algoritmusok módosítása, összekapcsolása, rugalmas átalakítása

Kreatív gondolkodás: kreatív, innovatív ötletek által mások megoldásaitól különböző, egyedi megoldások készítése a problémákra

Fontos, hogy az algoritmikus gondolkodás kialakításánál nagy gondot fordítsunk a rugalmasságra. Egy feladatot nem csak egyféle módon lehet megoldani. Ne csak a tanár által kigondolt megoldás legyen az előtérben, hanem biztosítsuk a tanulók megoldásainak az érvényesülését is! Nézzük meg a különböző megoldásokat, fedezzük fel a köztük lévő különbségeket, keressünk jobb algoritmust!

Korábbi kísérletek

Lénárd András az 1990-es évek elején negyedik osztályos tanulók algoritmikus gondolkodását mérte fel. Egy algofejtörőt kellett megoldani számítógépes program segítségével. A kísérlet eredménye azt mutatta, hogy a tanulók 16%-a csupán véletlenszerű próbálkozással igyekezett megoldani a feladatot, 14-19%-a viszont már ebben a korban is fejlett algoritmikus gondolkodással rendelkezett. Ebből kiindulva ennél akár fiatalabb korosztályban is érdemes kutatásokat végezni. Értékes információkat nyerhetünk akkor is, ha az oktatásban már régebb óta részt vevő tanulókat vonunk be a kutatásokba, mivel ők már egyfajta „megmerevedett” oktatási-tanulási szemlélettel rendelkeznek, így számukra az algofejtörők megoldása nem egy teljesen új, inkább az eddigiektől gyökeresen eltérő feladatformát jelenthet.

Órai tapasztalatok

Második osztály

Egy budai általános iskola második osztályában volt szerencsém megfigyelőként részt venni olyan órákon, ahol az algoritmussal és algofejtörő feladatokkal foglalkoztak.

A második osztályban első alkalommal a tanulók egyszerű, a hétköznapi életben is előforduló algoritmusokkal foglalkoztak. Első feladatként elmesélték, hogyan indul a napjuk a felkeléstől az iskolába történő elindulásig. A tanító piktogramokkal rögzített néhány történetet a táblán, utána a tanulók véleményezték. A felcserélt és a hiányzó lépéseket azonnal észrevették és a helyükre tették. Egy történet lépéseiből vicces reggelt alakítottak ki.

Következőleg a 3 perces lágy tojás készítésének lépéseit beszélték meg közösen. A tanulók kaptak egy papírt, melyen a következő lépések szerepeltek:

A feladatok megoldása folyamatos felügyelet és interaktív kérdez-felelek stílusban történt. A tanító kérdésekbe burkolt segítséggel vette rá a tanulókat, hogy a feladatok legfontosabb pontjait megbeszéljék. Például:

Tanító: Jó ez a recept?

Tanulók: Nem, hiányoznak lépések.

Tanító: Egészítsétek ki a receptet, hogy tényleg lágy tojást kapjunk eredményül!

A következő 7 lépésből álló megoldás született:

A tanulók egy percet kaptak a recept elolvasására, utána be kellett rakniuk a padba. A tanító a következő recept eredményére volt kíváncsi:

A tanulók felismerték, hogy mivel nem tettük bele a tojást a vízbe, ezért nyers tojás lesz az eredmény.

Újra elővehették a padban lévő papírt, amelyen szintén egy nyers tojás receptje volt. A tanulók felfedezték, hogy a lépések összekeveredésének következtében lett hibás a recept. A lépéseket önállóan megszámozták, a megoldáshoz használhatták a helyes receptet, végül közösen megbeszélték.

Második alkalommal két feladatot oldottak meg a tanulók. Italt vásároltak egy üdítő automatából, és megoldották egy szakasz katona átkelését a folyón. Az órán három darab hat fős csoportokban dolgoztak.

A tanító kivetítette egy italautomata képét az osztályteremben lévő TV-re. Megbeszélték, hogy ki milyen automatával találkozott már, és ki vásárolt is belőle. A tanulók többsége ismeri ezeket az automatákat (üdítő, rágó, kávé) és nagy részük vásárolt is belőle. A tanító elmondta, hogy most is hasonló feladatokat fognak megoldani, mint múlt órán a tojásfőzésnél.

Ismétlés képen újra elővették a receptet a következő módon: 7 tanuló kiállt a tábla elé, mindegyikük elmondott egy-egy lépést. A többiek lehajtották a fejüket, és a tábla előtt állók gyorsan helyet cseréltek, majd újra elmondták a lépéseiket. A tanulók rövid idő alatt helyreállították a megfelelő sorrendet. A második alkalommal, az egyik tanulót a tanító elbújtatta a teremben. Ebben az esetben is hamar megoldották a problémát.

Újra visszatértek a TV képernyőjére kivetített feladatra. A tanító röviden bemutatta az ábrát, a gombokat és azok helyét, felolvasta a feladatot, és a következő instrukciókat adta a gyerekeknek: „Írjátok le, hogy hogyan tudnátok üdítőt venni a gépből, használjátok a tojásfőzésnél tanult módszert! A feladat megoldására 10 perc áll rendelkezésetekre.” Az idő leteltével a megoldásokat közösen megbeszélték. Általánosan megfigyelhető, hogy a tanulók természetesnek vették, hogy az automata működik, és ugyan megnézték, hogy van-e a kiválasztott üdítőből, de csak azzal az esettel foglalkoztak, ha van.

A második feladatként a következő problémát kellett megoldaniuk:

Egy 5 főből álló katonai csapat egy folyóhoz érkezett, melyen szeretnének átkelni, de nem vezet át rajta híd, ugyanis lerombolták. A folyó mély, nem lehet rajta átgázolni. A parancsnok egyszer csak észrevesz két fiút, akik nem messze a parttól csónakáznak. A csónak azonban olyan kicsi, hogy abban vagy csak egy katona, vagy csak a két fiú tud átkelni, többen nem férnek bele. Végül is az összes katona átlelt a folyón csak ezzel az egy csónakkal. Hogyan szervezték meg az átkelést?

A tanító felolvasta a feladatot, és a következő megjegyzéseket fűzte hozzá:

Készült egy táblarajz a feladatról, mágneses korongokkal szemléltették a szereplőket, valamint a tanulók szóban elmondták, hogy a csónak milyen utasokkal közlekedhet (kettő gyerek, egy katona, egy gyerek). Az egyes eseteket a tanító a táblán mágneses korongokkal ábrázolta. A feladat megbeszélése után elkezdődött a munka. Öt percig dolgoztak, az első jó megoldás már 1,5-2 perc után megszületett. Egy csoportnak nem sikerült megoldania a feladatot, mert a feladat leírásával ellentétben kötelet használtak az átkelés során. A megoldásokat a táblánál minden csoportból 2 fő játszotta el. Az összes megoldás helyes volt, de a lépésszámok különböztek. A tanulók észrevették, hogy a hosszabb megoldás felesleges lépéseket tartalmaz.

Külön tanulsága a feladatnak, hogy bár a táblánál eljátszották, de papírra senkinek sem sikerült leírnia helyesen. A gyerekek mindkét órát nagyon élvezték, és mindenki aktívan részt vett a feladatok megoldásában.

Negyedik osztály

Az előbb említett budai általános iskolában, egy negyedikes osztályban is részt vettem megfigyelőként egy órán, ahol a következő három feladatot oldották meg önálló, illetve csoportmunka keretében.

Az első feladat ugyanaz volt, mint a második osztályban: ital vásárlása egy üdítő automatából. A tanulók megbeszélték a tanítóval, hogy ki találkozott és vásárolt már ilyen automatából. Az előzőekhez hasonlóan az automatát az egész osztály ismerte, és a többség vásárolt is belőle. A tanító interaktív kérdez-felelek stílusban ismertette a feladattal kapcsolatos fontosabb tudnivalókat. Például: Mennyibe kerül az üdítő? Hány forintom van? Mi célt szolgál a kijelző? Mi történik, ha több pénzt dobok be? A tanító a megoldás megkezdése előtt külön felhívta a gyerekek figyelmét arra, hogy vigyázzanak, mert ha egy lépés kimarad, nem kapják meg az üdítőt. A feladatot önállóan kellett megoldani, a rendelkezésre álló idő 5 perc volt. Az első megoldások 2-3 perc után megszülettek.

A megoldások többsége 3-4 négy lépésből állt, és ők is természetesnek vették, hogy a gép működik. Történtek esetszétválasztások az üdítő meglétével kapcsolatban, de csak az igen ággal foglalkoztak.

Második feladatként a földesurak és rabszolgáik átkelését kellett megoldaniuk:

Történt egyszer, hogy három földesúr három szolgájával egy folyón akart átkelni. A csónak, melyet a parton találtak, maximum 2 embert bírt el. A földesurak tartottak szolgáiktól, ezért az átkelést úgy kellett megoldaniuk, hogy egyik parton se legyenek a szolgák többségben. Hogyan birkóztak meg ezzel a feladattal a földesurak?

Közösen megbeszélték a fontosabb kérdéseket: Hányan akarnak átkelni a folyón? Mennyi a szolgák és földesurak létszáma? Hány embert bír el a csónak? Mikor vannak a szolgák többségben? Tisztázták, hogy sem kötelük, sem más eszközük nincsen, és úszni sem tudnak. A feladatot önállóan kellett megoldaniuk, rendelkezésre álló idő 10 perc volt.

A gyerekeknek gondot okozott a megoldások leírása. Inkább rajzoltak, ám ennek eredményei legtöbbször átláthatatlan és összenyilazott rajzok voltak.

Az utolsó feladattal 6 fős csoportokban próbálkoztak:

Egy napon Gremi nehéz helyzetbe került. Lement a pincébe gumibogyó szörpért. Talált ott egy 8 deciliteres kancsóval. Neki azonban csak 4 deciliterre volt szüksége. Szétnézett a pincében, hátha talál valami edényt, amivel ki tudja mérni a szükséges mennyiséget. Talált is egy 5 deciliteres és egy 3 deciliteres kancsót. Gremi elgondolkodott, hogyan tudna a kancsók segítségével 4 deciliter gumibogyó szörpöt kimérni. Elkezdte töltögetni a szörpöt egyik kancsóból a másikba, és végül sikerült neki kimérni. Hogyan mérte ki Gremi a 4 deciliter gumibogyó szörpöt, ha csak a 8 az 5 és a 3 deciliteres kancsókat használta, más eszközt, vagy mérőedényt nem?

A munka elkezdése előtt a tanító felhívta a tanulók figyelmét arra, hogy a 8 deciliteres kancsó tele van, a szörpöt nem lehet kiönteni, és nem folyhat ki a kancsókból. A feladattal 10 percig foglalkoztak. A tanulók között sétálva feltűnt, hogy mindenki annál a lépésnél akadt el, amikor mindhárom kancsóban van valamennyi szörp. Megkérdeztem tőlük, hogy két kancsó tartalmát össze lehet-e önteni. Ennek hatására megszületettek az első jó megoldások.

A megoldások rögzítésekor a legnagyobb problémát az okozta, hogy a tanulók mindig kiradírozták, hogy előzőleg mennyi szörp volt a kancsókban. Keveseknek jutott eszébe, hogy a különböző állapotokat külön rajzokon ábrázolja.

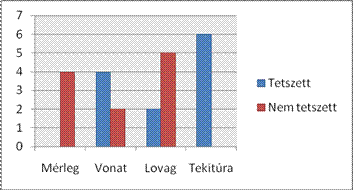
Az óra végén a tanítóval rövid közvélemény kutatást végeztünk, a feladatokkal kapcsolatban. A tanulóknak fele-fele arányban a földesuras és a kancsós feladat tetszett a legjobban. Azzal indokolták döntésüket, hogy ezeken a feladatokon lehetett gondolkodni, és rossz vagy hiányzó lépés esetén már nem jutottak el a megoldáshoz. Az automatás feladat azért nem nyerte el a tetszésüket, mert csak ismert lépéseket kellett leírni.

Egy pesti lakótelepi általános iskolában a tanítóval együttműködve tartottunk egy délutáni kétórás foglalkozást negyedikosztályosok számára. A foglalkozásra mágneses figurákat készítettem, és amíg zajlott a feladatok közös megbeszélése, én elkészítettem a táblán a feladatok ábráját.

Első feladatként, egy kétkarú mérleg segítségével kilenc külsőre teljesen egyforma golyó közül kellett kiválasztani a legnehezebbet. A tanítóval közösen beszélték meg a feladat megoldását. Elsőnek megvizsgálták azt az esetet, amikor 1-1 golyót teszünk a mérleg tányérjaiba, ilyenkor 4 mérés szükséges.

Tanító: Meg lehet-e oldani a feladatot kevesebb méréssel?

Tanulók: Igen, tegyünk a mérleg tányérjaiba 2-2 golyót

Tanító: Ekkor elegendő 3 mérés is.

Ezen felbuzdulva még rövidebb megoldást kerestek, jöttek a javaslatok 3 illetve 4 golyó mérésére is.

A második feladatban a következő vasutas példával találkoztak:

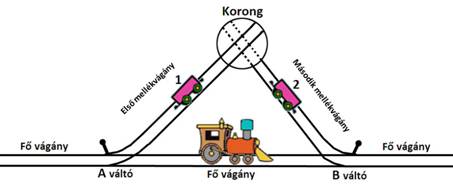
Az ábrán egy vasútállomás részlete látható. A fő vágányról elágazó két mellékvágány egy forgó koronggal van összekötve. A korong arra való, hogy az első mellékvágányról a második mellékvágányra (vagy fordítva) vigye a vasúti kocsikat. Egy hosszabb mozdony azonban már nem fér el a forgón. Az 1-es számú vagon az első mellékvágányon, a 2-es számú vagon a második mellékvágányon, a mozdony pedig a fő vágány A és B váltó közti sínszakaszon áll. Az A és B váltókon keresztül tudnak a vonatok a fő vágányról a mellékvágányra, és fordítva a mellékvágányról a fő vágányra menni. Az állomáson kapcsoló emberek is dolgoznak, akik a vasúti kocsik szét és összekapcsolását végzik. Hogyan viheti a mozdony az 1-es kocsit a 2-es kocsi helyére, a 2-es kocsit pedig az 1-es helyére, ha a mozdony nem fér rá a forgóra?

1. ábra.

Ennek a feladatnak az ábráját elkészítettem a táblán, melynek hatására a gyerekek kiszaladtak a táblához, és a bábuk pakolgatásával próbálták megoldani a problémát. Voltak jó ötletek, de nem hallgatták meg egymás javaslatait. Minden megoldásban beragadt a mozdony a korong és valamelyik kocsi közé. Ekkor segítettem annyit, hogy a mozdony egyszerre nem csak egy, hanem két kocsit is elbír. Újabb próbálkozások következtek, nagyon közel jártak a megoldáshoz, de még mindig beragadtak. A probléma ez alkalommal az volt, hogy a tanulók szerint a mozdony előröl, csak tolni tudja a kocsikat, húzni nem. A tévhit tisztázása után megbeszéltük a megoldást.

A következő feladatban három lovag, és fegyverhordozóinak átkelését kellett megoldaniuk:

Történt egyszer, hogy három lovag találkozott a folyóparton, mindegyiket a fegyverhordozója kísérte. Át akartak kelni a folyón a túlsó partra. A nádasban találtak egy kicsi, kétszemélyes csónakot. Az átkelés könnyűnek ígérkezett, hiszen a lovak át tudják úszni a folyót. Egy akadály azonban majdnem meghiúsította a vállalkozást. Az összes fegyverhordozó – mintha csak megállapodtak volna – kereken elutasította, hogy ismeretlen lovagok társaságában maradjon a saját gazdája nélkül. Sem rábeszélés, sem fenyegetés nem segített, a gyáva fegyverhordozók makacsul kitartottak álláspontjuk mellett. Végül az átkelést mégis megvalósították, mind a hat ember szerencsésen átjutott a túlsó partra egy kétszemélyes csónak segítségével. Az átkelés közben betartották a feltételt, amelyhez a fegyverhordozók ragaszkodtak. Hogyan keltek át a folyón, ha a kétszemélyes csónakon kívül más eszközük nem volt, és a lovak segítségét sem vették igénybe?

Ennél a feladatnál tisztázni kell a tanulókkal, hogy a lovak segítségét nem lehet igénybe venni, a lovakon kívül senki sem tud úszni, és nincs más eszközük (pl. kötelük). A megoldás kitalálása szintén táblánál zajlott figurák pakolgatásával. A gyerekek itt is elakadtak, de egy kis segítséggel eljutottak a megoldásig.

Utolsó feladatként egy Imagine-ben megírt programmal játszottak. A teknőst irányítva kellett megrajzolni két ábrát.

2. ábra.

A tanulók nagyon kevesellték az ábrák mennyiségét, mivel szívesen játszottak volna még a programmal, és szerintük az ábrák túl könnyűek voltak. A forgások számában általában voltak eltérések, de addig próbálkoztak, míg ki nem jött a legrövidebb megoldás. Miután már gombokkal kikísérletezték, hogy hogyan lehet az ábrát megrajzolni, szövegesen le tudták írni a megoldás lépéseit. Egy korábban végzett felmérésemben gép használata nélkül sokszor nem sikerült leírni a lépéseket.

Az óra végén végzett rövid közvélemény kutatás szerint, hogy melyik feladat tetszett a legjobban, az Imagine-ben írt Tekitúra névre keresztelt rajzolóprogram nyert, mert lehetett hozzá használni a számítógépet. Másodikként a vonatos példa nyerte el a tetszésüket, mert „jó gondolkodtató volt”.

A megoldások szöveges leírása, még akkor is komoly gondot jelentett, ha a megoldásokat előzőleg részletesen, közösen átbeszéltük. Szívesebben rajzoltak, de leginkább csak átláthatatlan, összenyilazott ábrák születtek.

3. ábra.

Konklúzió

Az eddigi tapasztalatom, hogy az említett korcsoport tanulói kifejezetten szeretik az algofejtörők megoldását könnyen, gyorsan és önszántukból kezdeményeznek csoportmunkát, bár a csoport önszervező és együttműködő képessége meglehetősen alacsony. Mindenképpen szükséges a korosztályhoz igazított megoldás rögzítési eszköz, a papíralapú szöveges rögzítés meghaladja e korcsoport képességeit. Élő tanórai alkalmazásban makettek, korongok, bábuk, alkalmazása, szerepek eljátszása jelenti a megoldást. Tanító felügyelete nélkül megfelelően megtervezett, interaktív, grafikus programfelület segítségével önálló munka is elérhető.

Tervek

Mivel úgy látom, hogy a nyomtatott felmérőkön keresztüli feladatmegoldás időigényes, és kevés eredménnyel járó metódus, és a tanulóknak is sokkal jobban tetszenek az interaktív megoldások, ezért egy web szerveres, böngészőn keresztül elérhető, adatbázist tartalmazó megoldás kifejlesztésén dolgozom.

Irodalom

1.  A. K. Dewdney: Számítógépes észjáték, Tudomány című folyóirat 1987/8. szám

2.  Szántó Sándor: Az algoritmikus gondolkodás fejlesztése
http://www.oki.hu/oldal.php?tipus=cikk&kod=2002-05-mu-Szanto-Algoritmikus

3.  Vassné Varga Edit: Algofejtörők – egy eszköz a gondolkodás fejlesztésére, Budapesti Tanítóképző Főiskola Tudományos közleményei XII., Budapest (1992) 71-86

4.  Vassné Varga Edit: Az algoritmikus gondolkodás fejlesztése és az informatikai alapismeretek, Oktatás-informatika 1988-89/2. szám 14-18


[1] Tudomány című folyóirat 1987/8. szám

[2] Szántó Sándor: Az algoritmikus gondolkodás fejlesztése az általános iskolában