Módszerek és eszközök a kriptográfia
oktatásakor
mgyongyi@ms.sapientia.ro
Sapientia Erdélyi Magyar Tudományegyetem, Románia
Absztrakt. Digitális világunkban naponta találkozunk olyan
alkalmazásokkal melyek többé-kevésbé kapcsolódnak a kriptográfiához. Éppen
ezért fontos megismernünk, hogy ezek hátterében milyen tudományos elméletek
állnak. Jelen dolgozat témája olyan korszerű matematikai és informatikai
eszközök és módszerek szemléltetése, melyek mind a felsőfokú oktatásban, mind a
középiskolában is alkalmazhatóak a kriptográfiai ismeretek elsajátítása
érdekében.
1. Bevezető
Mint minden tantárgy oktatásánál, a
kriptográfiai ismeretek elsajátításához is hasznos valamely már létező
szoftver, könyvtárcsomag alkalmazása. Ennek megválasztásában fontos szerepet
játszanak a minőségi és anyagi tényezők. A Sapientia Erdélyi Magyar
Tudományegyetemen is fontosak voltak ezen szempontok, amikor a gyakorlati
órákon alkalmas szoftvert választottuk ki.
Talán a legközismertebb, de nálunk
mégis kevésbé elterjedt szoftver a CrypTool, ([6]), melyet a németországi
Darmstadt Egyetemen kezdtek el fejleszteni a Deutsche Bank felkérésére. A kezdeti
cél az volt, hogy a bank a kliensei számára az adatbiztonsághoz kapcsolódó
fogalmakat közérthetővé tegye. Azóta ezt a szoftvert számos egyetemen,
középiskolában alkalmazzák a kriptográfiai ismeretek elsajátítására és ezen
egyetemi központok közül sokan részt is vállalnak a továbbfejlesztésben. A
szoftverben lehetőség van rejtjelezésre, visszafejtésre, digitális aláírás
generálására, protokollok lépésenkénti végigkövetésére, kriptoanalízis
kivitelezésére. Természetesen grafikus felülettel és részletes help-pel
rendelkezik, mely tartalmazza a kriptográfiához szükséges matematikai ismeretek
leírását, illetve a szoftver kezeléséhez szükséges ismereteket.
A kriptográfiai alapfogalmak elsajátítása történhet tehát egy specifikus szoftver alkalmazásával, de emellett fontos az alapalgoritmusokat valamely programozási nyelvben megírni, tesztelni, futtatni. Ehhez egy olyan programozási nyelv kell, amelyben a nagy számok kezelése nem jelent problémát, hiszen számos kriptográfiai algoritmusban több száz bites számokat kell kezelni. Nagy számok kezelésére alkalmas, szintén ingyenes könyvtárcsomag a C programozási nyelvhez a MIRACL, lásd [5], amit a CrypTool-ban is alkalmaznak a nagy számok aritmetikájához. Ezt a könyvtárcsomagot Windows és Linux alatt is lehet használni. Azoknak pedig, akik Javában szeretnek programozni, ott van az egyszerűen kezelhető BigInteger beépített osztály.
Kriptográfiai algoritmusok programozásához alkalmazhatóak még funkcionális programozási nyelvek is, például a Clean, ([4]) vagy Haskell, ([8]). Mindkettő esetében a nagy számok aritmetikájához szükséges műveletek egy könnyen kezelhető könyvtárcsomagban érhetőek el. Ezen nyelvek szintaxisa viszonylag egyszerűen elsajátítható és a kriptográfiai primitívek programozása legtöbb esetben követi a matematikai jelölésrendszert.
A fent említett módszerek mellett egy igazán szemléltető módszert
Koblitz alkalmaz, mikor a nagyközönségnek számítógép használata nélkül
magyarázza a nyilvános kulcsú kriptográfia működési elvét, ([3]).
Ebben dolgozatban ezen eszközöket
és módszereket mutatjuk be részletesebben.
2. A
CrypTool
A kriptográfia azok körében is nagy
érdeklődésnek örvend, akik nem rendelkeznek a szükséges matematikai
ismeretekkel, hiszen a kriptográfia most is - és már a kezdetekben is - a titok
tudománya volt. A titok megfejtése pedig köztudottan mindenki számára izgalmas
játék. Ezt a fajta misztériumot ki lehet és ki is kell használni, mikor a
kriptográfia oktatását elkezdjük. Egy rendszer feltörése, akkor is ha a
rendszer napjainkban már nem használatos, a diák előtt sokkal nagyobb
sikerélményt jelent, mint bármiféle matematikai ismeretek begyakoroltatása
rutin feladatokon keresztül. És ha a megfelelő kíváncsiság, a motiváció kialakult,
akkor a diák önszántából akarja elsajátítani a szükséges matematikai ismereteket. Éppen ezért évek óta olyan feladatokkal
indítjuk a gyakorlati órákat, melyek klasszikus rendszerek feltörésére
irányulnak. Erre írhatunk programot, de kiválóan alkalmas a CrypTool
programcsomag is, mely segítségével már az első laborokon elsajátíthatóak a
kriptoanalízis alapeszközei, mint például betűgyakoriság táblázat készítése
egy, két, három, stb. betűcsoport esetében, melyek megjelenítése történhet grafikusan,
vagy számadatokkal.
Legtöbbször első feladatként a
Keyword Caesar, az affin és Vigenere rendszerek feltörését szoktuk feladatul
kitűzni, mert ezek esetében a feltörés folyamata könnyebben vezet sikerhez, ([2]).
Ma már mindhárom rendszernek csak pedagógiai jelentősége van, de a szöveg rejtjelezéséhez,
a visszafejtéshez és a kriptoanalízishez már szükségesek elemi számelméleti
ismeretek (mint például a kiterjesztett Euklideszi algoritmus, kétismeretlenes
kongruenciarendszer megoldása, multiplikatív inverz meghatározása).
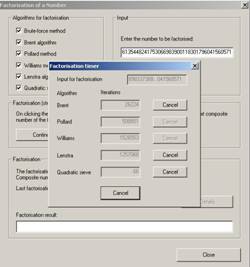
A kriptoanalízishez kapcsolódó másik példa, mely jól szemléltethető CrypTool-ban, az egész számok faktorizációjához kapcsolódik, ([1]). Az alábbi példa azt szemlélteti, hogy egy 200 jegyű összetett számot (ahol az összetett szám két prímszám szorzata) abban az esetben, mikor a két prím azonos nagyságrendű, azaz 100 bites szám, nem sikerül a programmal faktorizálni, de abban az esetben mikor a két prím eltérő nagyságrendű, azaz az egyik csak 20 bites, a másik pedig 180 bites szám, sikeres lesz a faktorizálás.
Legyenek a faktorizálandó számok:
Első eset:
X1 = 1008089371771445774355022807541 és
X2 = 891128717417623419588558134831,
melyeknek meghatározzuk a szorzatát, a kapott eredmény:
X =
898337388909026220826135448241753066983900118301796041560571.
Második eset:
X1 = 2239970412254013462458875877970941274024786565310505361 és
X2 = 1855891,
melyeknek meghatározzuk a szorzatát, a kapott eredmény:
X =
4157140928368513298856265612043368171991135163480679104931651.
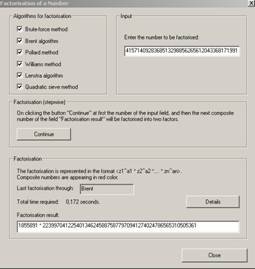
A CrypTool által megadott eredmények az alábbi két ablakban láthatóak, az első esetben látható, hogy a Pollard és Williams faktorizációs módszerek nem vezettek sikerre (nem aktívak a Cancel ablakok), a többiek esetében még a sokadik iteráció után sem kaptunk eredményt. A második ablakban a Brent faktorizációs módszer vezettet eredményre, 0.172 másodperc után.
|
|
|
A fenti példa arra is alkalmas, hogy az RSA nyilvános kulcsú kriptorendszer helytelen paraméter választására is felhívja a figyelmünket, azaz nem szabad olyan prímszámokat választani, amelyek nagyságrendje nagyon különbözik, mert ezek faktorizációjára léteznek hatékony algoritmusok.
Mindezen lehetőségek mellett a CrypTool programcsomag ennél jóval több szolgáltatást ad. Csak néhányat emelünk ki, csoportosítva őket témakörök szerint:
l Kriptográfiához kapcsolódó témakörök: klasszikus rendszerek, modern szimmetrikus rendszerek, aszimmetrikus rendszerek, hibrid rendszerek, digitális aláírás, kriptográfiai hash függvények, véletlen-szám generátorok működésének szemléltetése.
l Kriptoanalízishez kapcsolódó témakörök: a szimmetrikus rendszerek nyers-erő támadása, RSA elleni támadás, hibrid rendszerek elleni támadás, RSA-aláírás elleni támadás, kriptográfiai hash függvények elleni támadás kivitelezése.
l Pedagógiai eszközök, animációk: szimmetrikus és hibrid rendszerek, aláírás generálás, titokmegosztás, véletlen-számok 3D-s grafikus megjelenítése.
3. A
MIRACL
Mint a bevezetőben szó volt róla, a MIRACL oktatásra
ingyenes programcsomag, mely nagyszerűen alkalmazható valós kriptográfiai protokollok
kiépítésére, mert többek között a nagy számok aritmetikáját is tartalmazza.
1988 óta fejlesztik és számos kereskedelmi cég használja. Elsősorban a standard
C programozási nyelvhez készítették a megfelelő könyvtárakat, de legtöbbnek
megvan a C++ alá írt verziója is. Miután a diák vagy a kriptográfiával
ismerkedő személy kellőképpen megértette a szükséges alapfogalmakat, azok után
felmerülhet annak az igénye is, hogy valós alkalmazást készítsen. Ehhez minden
különösebb probléma nélkül felhasználhatja a MIRACL függvényeit.
Szemléltetésképpen itt is álljon egy példa, egy C program,
mely a MIRACL függvényeit alkalmazva meghatározza a Diffie-Hellman-kulcscsere
során generált kulcsokat, ([1]). Mielőtt megadnánk a C-ben megírt kódot,
röviden elmondjuk, hogy mit is jelent ez a protokoll. A korábban alkalmazott
rejtjelező algoritmusok legnagyobb problémája a rejtjelezéshez alkalmazott
kulcs, kommunikáló felek közötti megosztása volt. Ez a kulcscsere, melyet a
70-es években publikáltak, pedig lehetővé tette, hogy két legális és titkosan,
számítógépes hálózatban kommunikáló fél meg tudjon egyezni egy kulcsban, anélkül,
hogy fizikailag is találkoznának. A kulcscsere biztonsága azon az elven
alapszik, hogy a diszkrét logaritmus értékének meghatározására nem ismert
hatékony algoritmus, ha a kulcs szerepét játszó számok nagyságrendje kellőképpen
nagy. Feltételezve, hogy a kommunikációban részt vevő két legális fél Aliz és
Bob, a Diffie-Hellman-kulcscsere egyszerűsített protokollja a következő
lépéssorozatokból áll:
l
Aliz választ egy nagy
prímszámot, p-t, majd meghatározza p-nek egy primitív gyökét, legyen
ez q. Ezután választ egy
tetszőleges a pozitív egész számot,
ahol a<p-1. Majd
meghatározza az A = qa mod p értéket, ahol az a értékét titokban tartja, a p, q, A értékeket pedig elküldi
Bobnak.
l
Bob választ egy
tetszőleges b pozitív egész számot,
ahol b<p-1. Meghatározza a B = qbmod p értéket, a b értékét titokban tartja, B-t pedig elküldi Aliznak.
l
A közös kulcsot Aliz a
következőképpen határozza meg: K = Bamod p.
l
A közös kulcsot Bob a
következőképpen határozza meg: K = Abmod p.
l
Hogy a kulcsnak
mindkét fél ugyanazt az értéket kapja, azt a következő összefüggés biztosítja: K = Ab = Ba = ga∙bmod p.
Az alábbi programkódban a primtext változóban egy 309 számjegyű prímszámot adtunk meg, mely megfelel a fent megadott protokoll p-jének. A primitív gyök
értékének generálását az egyszerűség kedvéért az alábbi kódrészlet nem végzi
el, ezt 3-nak veszi. A A és B értékek meghatározását a powltr, a K értékek meghatározását
pedig a powmod könyvtárfüggvények végzik. A powltr-re optimalizálás miatt van szükség, mert a gyors
hatványozás ezen verziója hatékonyabb,
ha kis szám hatványra emelését kell elvégezni.
#include <stdio.h>
#include "miracl.h"
#include <time.h>
char
*primetext=
"155315526351482395991155996351231807220169644828378937433223838972232518351958838087073321845624756550146945246003790108045940383194773439496051917019892370102341378990113959561895891019716873290512815434724157588460613638202017020672756091067223336194394910765309830876066246480156617492164140095427773547319";
int main()
{
unsigned
long seed;
big a, b,
p, pa, pb, key;
miracl
*mip;
#ifndef MR_NOFULLWIDTH
mip =
mirsys(500,0);
#else
mip =
mirsys(500,MAXBASE);
#endif
a = mirvar(0);
b = mirvar(0);
p = mirvar(0);
pa = mirvar(0);
pb = mirvar(0);
key =
mirvar(0);
time((time_t *)&seed);
irand(seed);
printf("Diffie-Hellman
kulcscsere .... \n");
cinstr(p,primetext);
printf("\nAliz
eloszamitasai\n");
bigbits(160,a);
powltr(3,a,p,pa);
cotnum(pa, stdout);
printf("Bob
eloszamitasai\n");
bigbits(160,b);
powltr(3,b,p,pb);
cotnum(pb, stdout);
printf("az
Aliz altal meghatarozott kulcs=\n");
powmod(pb,a,p,key);
cotnum(key,stdout);
printf("A
Bob altal meghatarozott kulcs=\n");
powmod(pa,b,p,key);
cotnum(key,stdout);
return 0;
}
A tapasztalat azt mutatja, hogy ha
a diákok rendelkeznek megfelelő programozói ismeretekkel, akkor ezen
könyvtárfüggvények alkalmazása nem jelent gondot és könnyedén megtudják
írni a prímtesztelő, prím faktorizációs,
diszkrét logaritmus stb. meghatározását megvalósító algoritmusokat.
4. Funkcionális
programozási nyelvek
Érdekes
megfigyelés, hogy kriptográfiai algoritmusok kódja sokkal rövidebb valamely
funkcionális programozási nyelvben, mint egy imperatív programozási nyelvben mint
például C-ben vagy Java-ban. Ezen túlmenően egy funkcionális programozási
nyelvben megírt függvény tesztelése is jóval egyszerűbben megoldható. Már a
funkcionális programozási nyelv szintaxisa is arra készteti a programozót, hogy
moduláris kódokat írjon, melyekben a hibák javítása egyszerűbb. Hasonlóan
egyszerű a típushibák helyének meghatározása és kijavítása. A rekurzív algoritmusok
implementálása pedig szinte magától értetődő a funkcionális környezetben. Mi a
Clean programozási nyelvet tanítjuk, melyet a hollandiai nijmegeni egyetemen
fejlesztenek és ingyenes hozzáférésű. Rendelkezik nagy számok aritmetikáját
megoldó beépített modullal, ez a BigInt, melynek alkalmazása nem jelent különösebb problémát. A
nyelv I/O műveletei pedig egyszerűek, így ezek sem gátolják a programozó munkáját. A
szintaxis azt is lehetővé teszi, hogy a programozó a kriptográfiához szükséges
matematika helyes alkalmazására koncentráljon, és ne az implementálás
körülményeivel vesződjön.
Szemléltetésképpen
bemutatjuk a moduláris gyors hatványozást, mely számos kriptorendszerben
alapművelet. A moduláris hatványozás meghatározza az
xp (mod m) (1)
értékét, egy
gyors hatványozási technikával, ([1]), melynek először megadjuk a rövid leírását,
majd Clean-beli kódját.
A
moduláris hatványozást Clean-ben a my_exp és az lexp függvények alkalmazásával
valósítjuk meg, ahol a my_exp az inicializálásokat és az lexp segédfüggvény
meghívását végzi el. A tulajdonképpeni számításokat az lexp végzi. Ez a fajta megoldás, mely az inicializálásokat ilyen
formában adja meg teljes mértékben jellemző a funkcionális programozási nyelvekre.
Az lexp segédfüggvény bemeneti paraméterei az y, x, p, m értékek, ahol az x, p, m értékek az (1) képletnek megfelelőek, az y-ban pedig az eredményt számoljuk ki. A függvény minden egyes rekurzív hívása során
a következőket végezzük el:
l
ha a hatványkitevő
értéke 0, akkor megállunk, és
visszatérítjük az y értékét, egyébként
l
ha páratlan a kitevő,
akkor meghatározzuk az y = y∙x szorzatot
l
ha páros a kitevő,
akkor y értéke változatlan marad,
l
elvégezzük az x = x∙x négyzetre emelést (a szorzás és a négyzetre emelés
eredményeként kapott értékeket minden alkalommal mod m szerint vesszük)
l
elvégezzük a p = p/2, egész részt meghatározó osztás,
l
a következő rekurzív
hívás paraméterei az így kapott y, x, p értékek lesznek.
A továbbiakban
azon konstans értékek definícióját is megadjuk, melyeket a fent leírt két
függvény alkalmaz.
import BigInt
my_one :== toBigInt 1
my_two :== toBigInt 2
my_zero:== toBigInt 0
my_exp :: BigInt BigInt BigInt ->
BigInt
my_exp x p m = lexp my_one x p m
lexp :: BigInt BigInt BigInt BigInt
-> BigInt
lexp y x p m
|p ==
my_zero = y
#p1 = p /
my_two
#x1 = (x
* x) rem m
|isEven p
= lexp y x1 p1 m
#y1 = (y
* x) rem m
= lexp y1 x1 p1 m
Ezek alapján felmerült az a kérdés,
hogy a korábbi szokással ellentétben,
mely szerint a kriptográfia kizárólagos nyelve valamely imperatív nyelv
volt, nem lenne-e egyszerűbb és hatékonyabb,
hasonló biztonságú kriptográfiai alkalmazásokat valamely funkcionális programozási
nyelvben megírni. Ennek eredményeként a 2007/2008 egyetemi tanévben egy
államvizsgás diákunk azt a szakdolgozat témát kapta, hogy Kriptográfiai
algoritmusok funkcionális programozási környezetben,
melynek eredményeként sikeresen implementálta és tesztelte az RSA
kriptorendszert a Clean programozási nyelvben.
Hasonló elgondolás alapján kezdte
el fejleszteni a 2000-es évek elejétől a Cryptol programcsomagot az amerikai
Galois cég, ([7]). Ez tulajdonképpen egy programozási nyelv kriptográfiai alkalmazások
fejlesztésére, melyet a fejlesztők Haskell, ([8]) funkcionális programozási
nyelvben írtak. Próbaverziója ingyenesen hozzáférhető.
5. Számítógép
nélkül
A bevezetőben említettük, hogy léteznek
olyan elgondolások is, hogy a kriptográfiai alapelveket számítógépek használata
nélkül próbáljuk elsajátítani. Ennek a szemléltetésére egy matematikai modellen
keresztül bemutatjuk, hogy hogyan lehetséges nyilvános csatornán keresztül
pénzérme feldobálós játékot játszani, úgy hogy ne lehessen csalni, és ugyanakkor
hogyan lesz alkalmas a modell nyilvános kulcsú rejtjelezésre is. A feladat a
perfekt gráfokhoz kapcsolódik, ezért a diákoknak való bemutatás során el lehet
mondani egy-két gráfelméleti definíciót is.
Hasonlóan a harmadik fejezetben megadott szereposztáshoz,
most is Aliz és Bob fogják a pénzérme
feldobálós játékot játszani, ahol a következő lépéssorozatot végzik el:
l
Aliz választ egy n
csomópontú gráfot, majd kiválaszt k csomópontot, ezek fogják alkotni
a K halmazt. Tetszőlegesen összeköti a kiválasztott K-beli
csomópont mindegyikét valamelyik másik nem K-beli
csomóponttal. Az így kapott gráfot megjegyzi, ez lesz később a „bizonyíték”.
Majd további csomópontokat köt össze véletlenszerűen, de ezek egyike sem lehet K-beli
csomópont. Az így kapott gráfot elküldi
Bobnak. Aliz pénzérméjének értéke a „feldobás” után a K-beli
csomópontok párosságának értéke lesz.
l
Ezek után Bob tippel,
azaz jelzi, hogy Aliz páros vagy páratlan számra gondolt. Bob akkor nyer, ha az általa tippelt szám és
a K-beli csomópontok párossága megegyezik. Másképpen Aliz
nyer.
l
Miután Aliz megkapta Bob
válaszát, felfedi a K-beli csomópontokat, Bob pedig a kapott gráf alapján
könnyűszerrel ellenőrizni tudja, hogy Aliz nem csapta-e be.
Az 1., 2. és 3. ábrák mutatják, hogy Aliz miképpen
szerkeszti meg a „feldobásának” az értékét. Ez az érték a példa alapján 3 lesz.
A 4. ábrát küldi el Bobnak, mely után Bob tippel. Bob tehát, akkor nyer, ha
páratlan számot tippel.
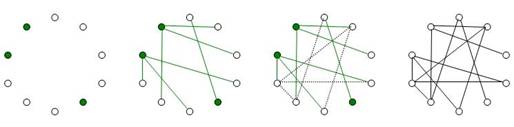
1. ábra 2.
ábra 3. ábra 4. ábra
A protokoll biztonsága, azaz hogy a felek nem tudnak
csalni, azon az elven alapszik, hogy a K-beli csomópontok perfekt gráfot
alkotnak és egy gráfban a perfekt gráfok csomópontjának a száma megegyezik.
Perfekt gráfot ily módon könnyű szerkeszteni, viszont a 4. ábra alapján kikövetkeztetni,
hogy mely csomópontok alkotnak perfekt gráfokat, azaz a perfekt gráfok meghatározása
tetszőleges gráfok esetében NP-beli nehézségű feladat.
Nyilvános kulcsú rejtjelezés során a rejtjelező (nyilvános kulcs) nem ugyanaz a
visszafejtő kulccsal (titkos kulcs), illetve a nyilvános kulcs ismerete alapján
gyakorlatilag lehetetlen meghatározni a titkos kulcsot. Mint említettük a perfekt
gráfok meghatározása, NP-beli feladat, ezért tökéletesen alkalmas nyilvános kulcsú
rejtjelezésre. A titkosításban résztvevő
felek legyenek megint Aliz és Bob, azzal a feltételezéssel, hogy Bob szeretne
titkos üzenetet küldeni Aliznak. A lépéssorozat
a következő lesz:
l
Aliz választ egy n
csomópontú gráfot, majd kiválaszt k csomópontot, ezek fogják alkotni
a K halmazt, (1. ábra). Tetszőlegesen összeköti a kiválasztott
K-beli csomópont mindegyikét valamelyik másik nem K-beli
csomóponttal. Az így kapott gráfot megjegyzi, ez lesz a titkos kulcs, (2. ábra).
Majd további csomópontokat köt össze véletlenszerűen, de ezek egyi ke sem lehet
K-beli csomópont, (3. ábra). Az így kapott gráfot nyilvánossá
teszi ez lesz a nyilvános kulcs, lásd 4. ábra.
l
Bob a nyilvános kulcs
alapján meghatározza a gráf csomópontjainak a számát. Feltételezve, hogy a
titkosítandó érték 25, első lépésben a 25 értékét meghatározza annyi szám
összegeként/különbségeként ahány csomópontú a gráf, (5. ábra). Az így kapott
számok fogják a csomópontok értékét jelenteni. Második lépésben minden
csomópontra meghatározza a csomópont értékének és a vele összekötött
csomópontok értékének az összegét, (6., 7. ábrák). Az így kapott gráf lesz a 25
rejtjelezett értéke, ezt elküld Aliznak.
l
A visszafejtéshez Aliz
meghatározza a K-beli csomópontok összegét, mellyel visszakapja a
titkosított értéket, (8. ábra).
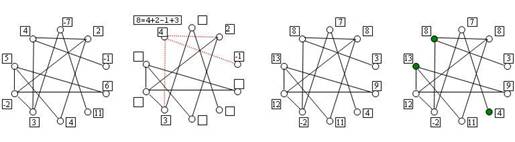
5. ábra 6. ábra 7. ábra 8. ábra
Természetesen bármilyen más grafikusan
is szemléltethető NP-beli feladat alkalmas a kriptográfiai fogalmak
megértésére. Befejezésként elmondhatjuk, hogy mindezen eszközök és módszerek
sikeresen alkalmazhatóak úgy az egyetemi oktatásban és a középiskolában is.
További terveink között szerepel, hogy a diákoktól kitöltött kérdőív formájában
kérjük azon visszajelzéseket, melyek alapján az ő véleményeiket is figyelembe
vehetjük a fenti eszközök és módszerek oktatásában.
Irodalom
1. Johannes Buchmann: Introduction to
cryptography. Springer-Verlag, (2002)
2. Arto Salomaa: Public-key cryptography, Berlin Heidelberg New-York, Springer-Verlag, (1996)
3. Tim Bell, Harold Thimbleby, Mike Fellows, Ian
Witten, Neil Koblitz: Explaining
cryptographic systems to the general
public. Computers and Education, Volume 40, Issue 3, (April 2003), 199-215
4. Pieter
Koopman, Rinus Plasmeijer, Marko van Eeklen, Sjaak Smetsers :Functional programming in Clean. http://clean.cs.ru.nl/contents/Clean_Book/clean_book.html
5. MIRACL: http://www.shamus.ie/
6. CrypTool: http://www.cryptool.org
7. Cryptol: http://www.cryptol.net
8. Haskell: http://www.haskell.org/