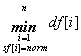Programozási tételek felsorolóra

Gregorics Tibor

Absztrakt. Ez a cikk a programtervezők által legismertebb programozási mintáknak, a programozási tételeknek a vizsgálatával foglalkozik. Lényeges kérdés az, hogy milyen formában lehet e tételeket megfogalmazni úgy, hogy kevés számú tétellel a feladatoknak viszonylag széles spektrumát megoldhassuk. Ebben a cikkben az ismert programozási tételeket felsoroló típusú objektumok feldolgozására mondjuk ki. Ehhez definiáljuk a felsoroló típus fogalmát, bemutatjuk az így nyert tételek robosztusságát, és rámutatunk arra is, hogy az így tervezett programok hogyan implementálhatóak a korszerű objektum orientált programozási környezetekben, C++, Java és C# nyelveken.

1. Bevezetés

A szoftverkészítés alapvető célja a megfelelő minőségű termékek előállítása. Ennek biztosításához különféle technológiákat, szabványokat alkalmazunk. Ezek között jelentős szerepe van az úgynevezett programozási mintáknak [1], amelyek a szoftver tervezése során feltárt egy-egy részproblémára adnak garantált minőségű megoldást. A programozási mintáknak több csoportját ismerjük: van amelyik a teszteléshez, a tesztadatok generálásához nyújt segítséget, mások az implementálást, a kódolást támogatják [2][3], több csoportjuk pedig a programtervezést. Ez utóbbiak között találjuk az úgynevezett tervmintákat, de a kisméretű részfeladatok megoldására kitalált algoritmus mintákat is, az úgynevezett programozási tételeket.

Egy programozási tétel egy általánosan megfogalmazott feladatból és az azt megoldó algoritmusból áll. Ha egy konkrét feladat a programozási tétel feladatához hasonló, akkor a programozási tétel algoritmusából, annak megfelelő átalakításával megkapjuk a konkrét feladat megoldását. [4] Ez a technika akkor garantálja legjobban az előállított megoldás helyességét, ha a feladatainkat formálisan fogalmazzuk meg, és meg tudjuk mutatni, hogy a konkrét (a megoldandó) feladat speciális esete a programozási tétel általános feladatának. Felfedve a konkrét és az általános feladat közötti különbségeket, elég ezeket a programozási tétel algoritmusára átvezetni, és annak algoritmikus újragondolása nélkül, mintha egy sablont töltenénk ki, kapjuk meg a konkrét feladatot megoldó programot. [5] Ezt a technikát hívjuk visszavezetésnek.[1][6]

A módszer használhatóságának lényeges feltétele a nem túl nagyszámú, ezért kellően általános, ugyanakkor nem is túl absztrakt, azaz a konkrét feladatokhoz jól illeszkedő programozási tételek gyűjteménye. A programtervezés módszertana kialakította már ezeknek a körét: az összegzés, számlálás, maximum kiválasztás, lineáris keresés, kiválasztás minden programozó számára ismert minták. Különbség csak abban van, hogy sokan tömbökre, mások intervallumon értelmezett függvényekre, megint másik relációs adatbázisra megfogalmazott feladatokként gondolnak ezekre a mintákra. De vajon meg kell különböztetni a programozási tételeket aszerint, hogy milyen adat felett fogalmazzuk meg őket? Nem lehet-e egységesen bevezetni e tételek úgy, hogy a túlzott általánosítás ne váljon a használhatóságuk rovására?

Ha egy adatot elemi értékek csoportja reprezentál, akkor az adat feldolgozásán többnyire annak elemi értékeinek feldolgozását értjük. Az ilyen adat típusának lényeges jellemzője, hogy az őt reprezentáló elemi értékeknek mi az egymáshoz való viszonya, a reprezentáció milyen jellegzetes belső szerkezettel rendelkezik, és hogy ebből fakadóan milyen sorrendben lehet az elemi értékeket bejárni. Számunkra különösen azok a típusok érdekesek, amelyek típusértékeit azonos típusú elemek sokasága alkotja, mint például egy tömb, egy halmaz vagy egy sorozat. Egy halmazból egymás után kivehetjük, egy sorozatnak vagy egy tömbnek végignézhetjük az elemeit. Éppen ezért az ilyen típusokat szokták felsorolhatónak (enumerable) vagy iteráltnak (iterált szerkezetűnek) nevezni, a példányaikat pedig gyűjteményeknek vagy tárolóknak (collection, container) hívni.

Felsorolni nemcsak iterált szerkezetű adatok elemeit lehet, hanem például egy egész szám valódi osztóit, vagy két egész szám által meghatározott zárt intervallum egész számait is. Ebből is látszik, hogy a felsorolás nem csak a felsorolhatósághoz kötődik. Általánosságban azt jelenti, hogy képesek vagyunk egy adatnak valamilyen értelemben vett első elemére ráállni, majd a soron következőre, meg tudjuk kérdezni, van-e egyáltalán első vagy soron következő elem, és lekérdezhetjük a felsorolás során éppen aktuális elemnek az értékét.

A felsorolást végző műveletek nem ahhoz az adathoz tartoznak, amelynek elemeit felsoroljuk, legfeljebb csak támaszkodnak az adat műveleteire. Furcsa is lenne, ha egy egész szám (amelyiknek valódi osztóira vagyunk kíváncsiak) alapból rendelkezne ilyen („vedd az első valódi osztót”, „vedd a következő valódi osztót”, „van-e még valódi osztó”, „mi az éppen vizsgált valódi osztó”) műveletekkel. De egy egész intervallumnak is csak olyan műveletei vannak, amivel az intervallum határait tudjuk lekérdezni, az intervallum egész számainak felsorolásához már egy speciális objektumra, egy indexre van szükség. Ráadásul egy intervallum felsorolása többféle lehet (egyesével vagy kettesével; növekvő, esetleg csökkenő sorrendben). A felsorolást végző műveleteket ezért mindig egy külön objektumhoz kötjük. Ha szükség van egy adat elemi érékeinek felsorolásra, akkor az adathoz hozzárendelünk egy ilyen felsoroló (bejáró) objektumot.

Egy felsoroló objektum feldolgozása azt jelenti, hogy az általa felsorolt elemi értékeket valamilyen tevékenységnek vetjük alá. Ilyen tevékenység lehet ezen értékek összegzése, adott tulajdonságú értékek megszámolása vagy a legnagyobb elemi érték megkeresése, stb. Ezek ugyanolyan feladatok, amelyek megoldására programozási tételeket vezetünk be, csakhogy most a szokásosnál általánosabb, felsorolóra kimondott változatukra van szükség. A programozási tételek felsorolókra történő általánosítását erősen motiválta az a gondolat, amelyet Bjarne Stroustrup így fogalmazott meg: „A bejáró (felsoroló) az a csavar, amely a tárolókat (gyűjteményeket) és az algoritmusokat összetartja. [7]

2. Felsoroló

Az alábbiakban bevezetjük a felsoroló objektumnak, mint a felsoroló típus egy példányának a fogalmát. Ismertetjük a felsoroló objektum általános feldolgozását végző algoritmust, majd néhány nevezetes felsorolót mutatunk be.

2.1. Felsoroló fogalma

Most általánosan jellemezzük az olyan objektumokat (ezeket hívjuk majd röviden felsorolónak), amelyek segítségével egy felsorolható adatnak (vektornak, halmaznak, szekvenciális inputfájlnak, valódi osztóit felkínáló természetes számnak) az elemeit egymás után elő lehet állítani.

Egy felsoroló objektum^{^[1]} (enumerator) véges sok elemi érték felsorolását teszi lehetővé azáltal, hogy rendelkezik a felsorolást végző műveletekkel: rá tud állni a felsorolandó értékek közül az elsőre vagy a soron következőre, meg tudja mutatni, hogy tart-e még a felsorolás és vissza tudja adni a felsorolás során érintett aktuális értéket. Ha egy típus ezeket a műveleteket biztosítja, azaz felsoroló definiálására képes, akkor azt felsoroló (enumerator) típusnak nevezzük.

Egy t felsoroló típusú objektum felsorolása mindig a t.First()^{^[2]} művelet végrehajtásával kezdődik, ez jelöli ki a felsorolás során először érintett elemi értéket (ha van ilyen egyáltalán). Minden további, tehát soron következő elemre a t.Next() művelet segítségével tudunk ráállni. A t.Current() művelet a felsorolás alatt kijelölt aktuális elem értéket adja meg. A t.End() függvény a felsorolás során mindaddig hamis értéket ad vissza, amíg van kijelölt aktuális elem, a felsorolás végét viszont igaz visszaadott értékkel jelzi. Fontos kritérium, hogy a felsorolás vége véges lépésben (a t.Next() véges sok végrehajtása után) bekövetkezzék. A felsoroló műveletek hatását általában nem definiáljuk minden esetre. Például nem-definiált az, hogy a t.First() végrehajtása előtt (tehát a felsorolás kezdete előtt) illetve a t.End() igazra váltása után (azaz a felsorolás befejezése után) mi a hatása a t.Next(), a t.Current() és a t.End() műveleteknek. Álatlában nem definiált az sem, hogy mi történjen, ha a t.First() műveletet a felsorolás közben ismételten végrehajtjuk.

Minden olyan típust felsorolónak nevezünk, amely megfelel a felsoroló típus-specifikációnak, azaz implementálja a First(), Next(), End() és Current() műveleteket.

A felsoroló (enumerator) típust enor(E)-vel jelöljük, ahol az E a felsorolt elemi értékek típusa. Ezt a jelölés alkalmazhatjuk a típus értékhalmazára is. Egy felsoroló objektum hátterében mindig elemi értékeknek azon véges hosszú sorozatát kell látnunk, amelynek elemeit sorban, egymás után be tudjuk járni, fel tudjuk sorolni. Ezért specifikációs jelölésként megengedjük, hogy egy t felsoroló által felsorolható elemi értékre úgy hivatkozzunk, mint egy véges sorozat elemeire: a t_i a felsorolás során i-edikként felsorolt elemi érték, ahol i az 1 és a felsorolt elemek száma (jelöljük ezt |t|-vel) közé eső egész szám. Hangsúlyozzuk, hogy a felsorolható elemek száma definíció szerint véges. Ezzel tulajdonképpen egy absztrakt megvalósítást is adtunk a felsoroló típusnak: a felsorolókat a felsorolandó elemi értékek sorozata reprezentálja, a felsorolás műveleteit a sorozat bejárásával implementáljuk.

A felsoroló típus konkrét reprezentációjában mindig megjelenik valamilyen hivatkozás arra az adatra, amelyet felsorolni kívánunk. Ez lehet egyetlen természetes szám, ha annak az osztóit kell előállítani, lehet egy tömb, szekvenciális inputfájl, halmaz, esetleg multiplicitásos halmaz (zsák), ha ezek elemeinek felsorolása a cél, vagy akár egy gráf, amelynek a csúcsait valamilyen stratégiával be kell járni, hogy az ott tárolt értékekhez hozzájussunk. A reprezentáció ezen az érték-szolgáltató adaton kívül még tartalmazhat egyéb, a felsorolást segítő komponenseket is. A felsorolás során mindig van egy aktuális elemi érték, amelyet az adott pillanatban lekérdezhetünk. Egy egydimenziós tömb, azaz egy vektor elemeinek felsorolásánál ehhez elég egy indexváltozó, egy szekvenciális inputfájl esetében a legutoljára kiolvasott elemet kell tárolni illetve, azt, hogy sikeres volt-e a legutolsó olvasás, az egész szám osztóinak felsorolásakor például a legutoljára megadott osztót.

2.2. Felsorolók bejárása

A felsoroló által visszaadott értékeket rendszerint valahogyan feldolgozzuk. Ez a feldolgozás igen változatos lehet; jelöljük ezt most általánosan az F(e)-vel, amely egy e elemi értéken végzett tetszőleges tevékenységet takar. Nem szorul különösebb magyarázatra, hogy a felsorolásra épülő feldolgozást az alábbi algoritmus-séma végzi el. Megjegyezzük, hogy mivel a felsorolható elemek száma véges, ezért ez a feldolgozás véges lépésben garantáltan befejeződik.

t.First()
Øt.End()
	F( t.Current() )
	t.Next()

2.3. Nevezetes felsorolók

Az alábbiakban megvizsgálunk néhány fontos felsoroló típust, olyat, amelynek reprezentációja valamilyen nevezetes – egy kivételével – iterált típusra épül. Természetesen minden esetben ki fogunk térni arra, hogy a vizsgált típus hogyan feleltethető meg a felsoroló típusspecifikációnak, azaz mi a felsorolást biztosító First(), Next(), End() és Current() műveletek implementációja. Vizsgálatainknak fontos része lesz, hogy megmutatjuk egy-egy konkrét felsoroló típusú objektum esetén hogyan módosul az előbb bemutatott általános feldolgozást végző algoritmus-séma.

Tekintsük először az egész-intervallumot felsoroló típust, amely egy [m..n] intervallum elemeinek klasszikus, m-től n-ig egyesével történő felsorolását végzi. Természetesen ennek mintájára lehet definiálni a fordított sorrendű vagy a kettesével növekedő felsorolót is. Az egész számok intervallumát nem tekintjük iterált szerkezetűnek, hiszen a reprezentációjához elég az intervallum két végpontját megadni, műveletei pedig ezeket az intervallumhatárokat kérdezik le. Ugyanakkor mindig fel lehet sorolni az intervallumba eső egész számokat. Az egész-intervallumra épülő felsoroló típus attól különleges számunkra, hogy a programozási tételek ismertebb változatait az egész számok egy intervallumára (amely lehet egy vektor indextartománya is) szokták megfogalmazni, így ez a bizonyítéka annak, hogy az általunk bevezetendő tételek valóban általánosításai az informatikusok többsége által ismert tételeknek.

A felsoroló típus egy típusértékét egy [m..n] intervallum két végpontja (m és n) és az intervallum elemeinek felsorolását segítő egész értékű indexváltozó (i) reprezentálja. Az i változó az [m..n] intervallum aktuálisan kijelölt elemét tartalmazza, azaz implementálja a Current() függvényt. A First() műveletet az i:=m értékadás, a Next() műveletet az i:=i+1 értékadás váltja ki. Az i>n helyettesíti az End() függvényt. (A First() művelet itt ismételten is kiadható, és mindig újraindítja a felsorolást, mind a négy művelet bármikor, a felsoroláson kívül is terminál.)

Ezek alapján a felsoroló objektum feldolgozását végző általános algoritmus-sémából előállítható az egész-intervallum normál sorrendű feldolgozását végző algoritmus, amelyet természetesen számlálós ciklus formájában is megadhatunk.

i:=m
i£n
	F(i)
	i:=i+1

Könnyű végiggondolni, hogy miként lehetne az intervallumot fordított sorrendben ( i:=n, i:=i-1, i<m), vagy kettesével növekedően (i:=m, i:=i+2, i>n) felsorolni.

Magától értetődően lehet sorozatot felsoroló típust készíteni. (Itt is a klasszikus, elejétől a végéig tartó bejárásra gondolunk, megjegyezve, hogy más bejárások is vannak.) A reprezentáció ilyenkor egy sorozat típusú adat (s) mellett még egy indexváltozót (i) is tartalmaz. A sorozat (elejétől végéig történő) bejárása során az i egész típusú indexváltozót az 1 .. |s| intervallumon kell végig vezetni éppen úgy, ahogy ezt az előbb láttuk. Ekkor az s_i-t tekinthetjük az Current() kifejezésnek, az i:=1 a First() művelet lesz, az i:=i+1 a Next() művelet megfelelője, az i>|s| pedig az End() kifejezéssel egyenértékű. (A First() művelet ismételten is kiadható, és mindig újraindítja a felsorolást, a Next() és End() bármikor befejeződik, de a Current()csak a felsoroláson alatt terminál.) Ezek alapján az s sorozat elemeinek elejétől végéig történő felsorolását végző programot az alábbi két alakban írhatjuk fel.

i:=1
i£\|s\|
	F(s_i)
	i:=i+1

A vektort (klasszikusan) felsoroló típus a sorozatokétól csak abban különbözik, hogy itt nem egy sorozat, hanem egy v vektor bejárása a cél. A bejáráshoz használt indexváltozót (jelöljük ezt most is i-vel) a bejárandó v vektor indextartományán (jelöljük ezt [m..n]-nel) kell végigvezetünk, és az aktuális értékre a v[i] formában hivatkoznunk. Ennek értelmében az v[i]-t tekinthetjük a Current() műveletnek, az i:=m tulajdonképpen a First() művelet lesz, az i:=i+1 a Next() művelet megfelelője, az i>n pedig a End() kifejezéssel egyenértékű. (A First() művelet ismételten is kiadható, és mindig újraindítja a felsorolást, a Next() és End() bármikor befejeződik, de a Current()csak a felsoroláson alatt terminál.) Egy vektor elemeinek feldolgozását számlálós ciklussal szokás megadni:

i:=m .. n
	F(v[i])

Mivel a mátrix vektorok vektora, ezért nem meglepő, hogy mátrixot (sorfolytonosan) felsoroló típust is lehet készíteni. Ez a mátrix esetén az egyik leggyakrabba alkalmazott felsorolás, amikor először az első sor elemeit, azt követően a másodikat, és így tovább, végül az utolsó sort járjuk be. Egy n*m-es a jelű mátrix ilyen sorfolytonos bejárásánál a mátrixot felfoghatjuk egy n*m elemű v vektornak, ahol minden 1 és n*m közé eső k egész számra a v[k] = a[((k-1) div m) +1, ((k-1) mod m) +1]. Ezek után a bejárást a vektoroknál bemutatott módon végezhetjük. Egyszerűsödik a fenti képlet, ha a vektor és a mátrix indextartományait egyaránt 0-tól kezdődően indexeljük. Ilyenkor v[k] = a[k div m, k mod m], ahol a k a 0..n*m-1 intervallumot futja be.

A mátrix elemeinek sorfolytonos bejárása így igen egyszerű lesz, bár nem ez az általánosan ismert módszer. (Ezt számlálós ciklus segítségével adjuk meg)

k=0 .. n*m-1
	F(a[k div m, k mod m])

Mivel a mátrix egy kétdimenziós szerkezetű típus, ezért a bejárásához két indexváltozót szoktak használni. (Más szóval a mátrix bejárót egy mátrix és két indexváltozó reprezentálja.) Sorfolytonos bejárásnál az egyiket a mátrix sorai közötti bejárásra, a másikat az aktuális sor elemeinek a bejárására használjuk. A bejárás során a[i,j] lesz a Current(). Először a a[1,1]-re kell lépni, így a First() műveletet az i,j:=1,1 implementálja. A soron következő mátrixelemre egy elágazással léphetünk rá. Ha a j bejáró még nem érte el az aktuális sor végét, akkor azt kell eggyel megnövelni. Ellenkező esetben az i bejárót növeljük meg eggyel, hogy a következő sorra lépjünk, a j bejárót pedig a sor elejére állítjuk. Összességében tehát az IF(j£m: j:=j+1; j>m: i,j:=i+1,1) elágazás implementálja a Next() műveletet. Az End() kifejezést az i>n helyettesíti.

i,j:=1,1
i£n
	F( a[i,j] )
	j£m
	j:=j+1	i,j:=i+1,1

Ennek a megoldásnak egy „trükkös”, de a gyakorlatban sokkal jobban ismert változata az alábbi kétciklusos algoritmus. Itt az i,j:=1,1 értékadást (First()) a két egymásba ágyazott ciklus inicializáló lépése végzi el. A Next() műveletet megvalósító elágazás feltétele (j£m) a belső ciklus ciklusfeltétele lesz, a belső ciklus ciklusmagja pedig a megfelelő programág (j:=j+1). Az elágazás másik ága a belső ciklus befejeződése után (tehát j>m esetben) hajtódik végre: először a külső ciklus magjának végén az i:=i+1, majd a ciklusmag ismételt futtatásának elején, a belső ciklus indexváltozójának inicializálása (j:=1) során történik meg. Természetesen ezt a két egymásba ágyazott ciklust számlálásos ciklusként érdemes leírni.

i=1 .. n
	j=1 .. m
		F( a[i,j] )

A szekvenciális inputfájl felsoroló típusa egy szekvenciális inputfájllal (f), egy elemi értékkel (e), és egy státusszal (st) reprezentál egy bejárót. A szekvenciális inputfájlnak (jelölése: infile(E)) ugyanis egyetlen művelete van: a sorozat első elemének lefűzése, más szóval az olvasás művelete. Matematikai értelemben ez egy olyan függvény, amely egy sorozat típusú objektumhoz (pontosabban az őt reprezentáló sorozathoz) három értéket rendel: az olvasás státuszát, a sorozat első elemét (ha van ilyen), és az első elemétől megfosztott sorozatot. Az olvasást az st,e,f:=read(f) értékadással, vagy rövidítve az st,e,f:read szimbólummal jelöljük. Itt az st az olvasás státuszát kapja. Ez egy speciális kételemű halmaznak (Státusz ={abnorm, norm}) az egyik eleme. Ha az f eredeti értéke egy üres sorozat volt, akkor az st változó az abnorm értéket veszi fel, különben a norm-ot. Ha az f-beli eredeti sorozat nem üres, akkor az e az eredeti sorozat első elemét, az f az eggyel rövidebb sorozatot veszi fel, egyébként az f-beli sorozat továbbra is üres marad, az e pedig definiálatlan. A szekvenciális inputfájl felsorolása csak az elejétől végéig történő olvasással lehetséges, amelyhez ezt a read műveletet használhatjuk.

st, e, f : read
st=norm
	F(e)
	st, e, f : read

A First() műveletet az először kiadott st,e,f:read művelet váltja ki. Ez az aktuális elemet az e segédváltozóba teszi, így a Current() helyett közvetlenül az e értékét lehet használni. A read művelet mindig értelmezett, de a bejárást nem lehet ismételten elindítani vele. Az ismételten kiadott st,e,f:read művelet ugyanis már az f.Next() művelettel egyenértékű. Az f.End() az olvasás sikerességét mutató st státuszváltozó vizsgálatával helyettesíthető. (Mind a négy művelet minden esetben, a felsoroláson kívül is terminál.)

A halmazt felsoroló típus reprezentációjában egy a felsorolandó elemeket tartalmazó h halmaz szerepel. Ha a h=Æ, akkor a halmaz bejárása nem lehetséges vagy nem folytatható – ez lesz tehát az End() művelet. Ha a h¹Æ, akkor könnyen kiválaszthatjuk felsorolás számára a halmaznak akár az első, akár soron következő elemét. Természetesen az elemek halmazbeli sorrendjéről nem beszélhetünk, csak a felsorolás sorrendjéről. Ez az elemkiválasztás elvégezhető a nem-determinisztikus e:Îh értékkiválasztással éppen úgy, mint a halmazokra bevezetett determinisztikus elemkiválasztással (e:=mem(h)). Mi ez utóbbit fogjuk a Current() művelet megvalósítására felhasználni azért, hogy amikor a halmaz bejárása során tovább akarunk majd lépni, akkor éppen ezt, a felsorolás során előbb kiválasztott elemet tudjuk majd kivenni a halmazból. Ehhez pedig pontosan ugyanúgy kell tudnunk megismételni az elemkiválasztást. A Next() művelet ugyanis nem lesz más, mint a mem(h) elemnek a h halmazból való eltávolítása, azaz a h:=h–{mem(h)}. Ennek az elemkivonásnak az implementációja egyszerűbb, mint egy tetszőleges elem kivonásáé, mert itt mindig csak olyan elemet veszünk el a h halmazból, amely biztosan szerepel benne, ezért ezt külön nem kell vizsgálni. A Next() művelet is (akárcsak a Current()) csak a bejárás alatt – azaz amíg az End() hamis – alkalmazható. Láthatjuk azonban, hogy sem az End(), sem a Current(), sem a Next() művelet alkalmazásához nem kell semmilyen előkészületet tenni, azaz a felsorolást elindító First() művelet halmazok bejárása esetén az üres (semmit sem csináló) program lesz.

Ezen megjegyzéseknek megfelelően a halmaz elemeinek feldolgozását az alábbi algoritmus végzi el:

h¹Æ
	F(mem(e))
	h := h – {mem(e)}

3. Felsorolóra megfogalmazott programozási tételek

Az alábbiakban bemutatott általános programozási tételekben nem közvetlenül a felsorolt elemeket dolgozzuk fel (adjuk össze, számoljuk meg, stb.), hanem az elemekhez hozzárendelt értékeket. Ezeket bizonyos tételeknél (pl. összegzés, maximum kiválasztás) egy f:E→H függvény (ez sokszor lehet az identitás), másoknál (pl. számlálás, keresés) egy b:E→L logikai függvény jelöli ki. amely a felsorolt értékekhez rendeli a feldolgozás alapját képező értékeket. Ennek következtében a feldolgozás során általában nem a t.Current() értékeket, hanem az f(t.Current()) vagy b(t.Current()) értékeket kell vizsgálni.

A maximum kiválasztásnál, a feltételes maximum keresésnél, a kiválasztásnál és a lineáris keresésnél célszerű bevezetni egy-egy új specifikációs jelölést. Mind a négy esetben megadjuk ugyan az utófeltétel eredeti formuláját is, amelyről azonban látszik, hogy a visszavezetés szempontjából sok lényegtelen elemet tartalmaz. Ezért indokolt a rövidített jelölések használata.

3.1. Összegzés

Feladat: Adott egy enor(E) felsoroló típusú t objektum és egy f:E→H függvény. A H halmazon értelmezzük az összeadás asszociatív, baloldali nullelemes műveletét. Határozzuk meg a függvénynek a t elemeihez rendelt értékeinek összegét, azaz a kifejezés értékét! (Üres objektum esetén az összeg értéke definíció szerint a nullelem: 0).

Specifikáció:

A = ( t:enor(E), s:N )
Ef = ( t=t’ )
Uf = (s =)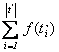

Algoritmus:

s := 0 t.First()
Øt.End()
	s := s + f(t.Current())
	t.Next()

3.2. Számlálás

Feladat: Adott egy enor(E) felsoroló típusú t objektum és egy b:E®L feltétel. Határozzuk meg, hogy a felsoroló objektum elemi értékei közül hányra teljesül a feltétel.

Specifikáció:

A = ( t:enor(E), c:N )
Ef = ( t=t’)
Uf = ()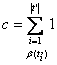

Algoritmus:

c:=0 t.First()
Øt.End()
	b( t.Current() )
	c:=c+1	SKIP
	t.Next()

3.3. Maximum kiválasztás

Feladat: Adott egy enor(E) felsoroló típusú t objektum és egy f:E→H függvény. A H halmazon definiáltunk egy teljes rendezési relációt. Feltesszük, hogy t nem üres. Határozzuk meg a függvénynek a t elemeihez rendelt értékei között a maximálisat.

Specifikáció:

A = ( t:enor(E), max:H, elem:E )
Ef = ( t=t’ Ù |t|>0 )
Uf = (max = f(elem) = Ù elemÎ t’)

Algoritmus:

t.First()
max, elem:= f(t.Current()), t.Current()
t.Next()
Øt.End()
	f(t.Current())>max
	max, elem:= f(t.Current()), t.Current()	SKIP
	t.Next()

3.4. Feltételes maximum keresés

Feladat: Adott egy enor(E) felsoroló típus t objektum és egy f:E→H függvény. A H halmazon definiáltunk egy teljes rendezési relációt. Adott továbbá egy b:H®L feltétel. Határozzuk meg t azon elemeihez rendelt f szerinti értékek között a maximálisat, amelyek kielégítik a b feltételt.

Specifikáció:

A = ( t:enor(E), l:L, max:H, elem:E )
Ef = ( t=t’)
Uf = ((l= $iÎ[1.. |t’|]: b(t’_i) ) Ù (l ® max=f(elem) = 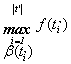) Ù elemÎ t’))

Algoritmus:

l:= hamis; t.First()
Øt.End()
	Øb(t.Current())	b(t.Current()) Ù l		b( t.Current()) Ù l
	SKIP	f(t.Current())>max		l, max, elem := igaz, f(t.Current()), t.Current()
		max, elem:= f(t.Current()), t.Current()	SKIP
	t.Next()

3.5. Kiválasztás

Feladat: Adott egy enor(E) felsoroló típusú t objektum és egy b:E®L feltétel. Keressük a t bejárása során az első olyan elemi értéket, amely kielégíti a b:E®L feltételt, ha tudjuk, hogy biztosan van ilyen.

Specifikáció:

A = ( t:enor(E), elem:E )
Ef = ( t=t’ Ù $iÎ[1.. |t|]: b(t_i) )
Uf = ($iÎ[1.. |t’|]: Ù b(elem) Ù "jÎ[1..i-1]: Øb() )

Algoritmus:

t.First()
Øb(t.Current())
	t.Next()
elem:=t.Current()

3.6. Lineáris keresés

Feladat: Adott egy enor(E) felsoroló típusú t objektum és egy b:E®L feltétel. Keressük a t bejárása során az első olyan elemi értéket, amely kielégíti a b:E®L feltételt.

Specifikáció:

A = ( t:enor(E), l:L, elem:E )
Ef = ( t=t’)
Uf = ( (l=$iÎ[1.. |t’|]:b(t_i)) Ù
(l ® $iÎ[1.. |t’|]: Ù b(elem) Ù "jÎ[1..i-1]: Øb()) )

Algoritmus:

l := hamis; t.First()
Øl Ù Øt.End()
	elem := t.Current()
	l := b(elem)
	t.Next()

3.7. Rekurzív függvény helyettesítési értéke

Feladat: Adott egy enor(E) felsoroló típusú t objektum és egy f:Z®H k-ad rendű 1 bázisú rekurzív függvény (k pozitív egész szám) úgy, hogy f(i) = f(t_i, f(i–1), ... ,f(i–k) ) ahol i≥1 és a f egy E×H^k®H függvény, továbbá f(m–1)=e_m–1, ... , f(m–k)= e_m–k, ahol e_m-1, ... , e_m–k H-beli értékek. Számítsuk ki az f függvény |t| helyen felvett értékét!

Specifikáció:

A = ( t:enor(E), y:H )
Ef = ( t=t’ )
Uf = ( y=f(|t’|) )

Algoritmus:

y, y₁, ... , y_k_–1 := e_m–1, e_m–2, ... , e_m–k ; t.First()
Øt.End()
	y, y₁, y₂,... , y_k_–1 := f(t.Current(), y, y₁, ... , y_k_–1), y, y₁, ... , y_k_–2
	t.Next()

4. Értékelés

A tervezéshez használt programozási minták megítélésénél két szempontot kell figyelembe venni. Egyik szempont a robosztusság, azaz hogy a minták minél általánosabb legyenek, sok probléma megoldásához nyújtsanak segítséget. A minták száma azonban nem lehet túl sok, a megfogalmazásuk pedig nem lehet túl absztrakt. A programozási tételeink száma, absztrakciós szintje már elég sok próbát kiállt. Itt nekünk csak azt kell igazolni, hogy a felsorolókra kimondott változataik – amelyek kétség kívül általánosabbak a programozó társadalomban jobban ismert tömbökre vagy intervallumon értelmezett függvényekre kimondott fajtáknál – nem túl általánosak-e. Erre legmeggyőzőbb választ az alkalmazásaikkal adhatunk. A programozási minták értékelésének másik szempontja, hogy a segítségükkel előállt tervek mennyire könnyen implementálhatók egy konkrét programozási környezetben.

4.1. Robosztusság

A most bevezetett tételek segítségével egyszerűvé válik az olyan feladatok megoldása, amelyek felsorolt értékek összegzését, megszámolását, maximum-kiválasztását vagy keresését írják elő. Ha a specifikációjában rámutatunk arra, hogy milyen felsorolóra vonatkozik a feladat (hogyan kell implementálni a First(), Next(), End() és Current() műveleteket) és milyen programozási tétel alapján kell a felsorolt értékeket feldolgozni (mi helyettesíti az adott programozási tételben szereplő függvényt, függvényeket), akkor visszavezetéssel megkaphatjuk a megoldást.

A felsorolókra általánosított programozási tételekre könnyen visszavezethetők az olyan feladatok, ahol egy nevezetes gyűjtemény nevezetes felsorolója jelenik meg a háttérben. Az alábbi feladatok megoldásai (amelyeket egyszerűségük miatt nem részletezünk) jól illusztrálják, hogy a fentiekkel milyen erős eszközt kaptunk a módszeres programtervezés számára. Halmaz bejárásával oldható meg például a „Keressük meg a halmaz maximális elemét!” (maximum kiválasztás) vagy „Számoljuk meg egy halmazbeli szavak között, hogy hány ’a’ betűvel kezdődő van!” (számlálás) feladat. Szekvenciális inputfájl bejárására van szükség a „Keressük meg egy szekvenciális inputfájl első nem-negatív elemét!” (lineáris keresés) feladatnál. Mátrix elemeinek felsorolását igényli az „Adjuk meg egy egész elemű mátrix egyik maximális elemét és annak indexeit!” vagy „Keressünk egy egész elemű mátrixban egy páros számot és adjuk meg annak indexeit!” feladat. Összegzéssel lehet megoldani másolás, kiválogatás és szétválogatás jellegű feladatokat.

Érdekesebbek azok a feladatok, ahol egyedi felsorolót kell bevezetni a megoldáshoz. Ilyen az alábbi feladat: Határozzuk meg egy n pozitív egész szám prímosztóinak az összegét!

Először úgy specifikáljuk a feladatot, hogy az egy intervallum felsorolására épített feltételes összegzés legyen, ahol a feltételhez el kell dönteni, hogy egy szám prím-e.

A = (n:N , sum:N)
Ef = ( n=n' )
Uf = ( Ef Ù sum = )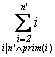

A feladat ügyesebb megoldásához jutunk, ha átfogalmazzuk azt egy egyedi felsoroló segítségével. Képzeljük el azt a felsorolót, amelyik t, amely közvetlenül az n szám prím osztóit sorolja fel.

A = (t:enor(N), s:N)
Ef = ( t=t')
Uf = ( Ef Ù sum = )

Ezt visszavezethetjük az összegzésre úgy, hogy abban az E=H=N és minden e természetes számra f(e)= e.

sum := 0 t.First()
Øt.End()
	sum := sum + t.Current()
	t.Next()

Látjuk, hogy a visszavezetés érdekében a feladatot egy másik állapottéren újraspecifikáltuk, ahol a t felsorolót az n adat helyett vezettük be, ezért kézenfekvőnek látszik, hogy a felsorolót az n segítségével reprezentáljuk. Az n szám ugyanis implicit módon az összes prímosztóját tartalmazza. Ha n legalább 2, akkor ezek közül az egyikhez, mondjuk a legkisebbhez, úgy jutunk hozzá, ha egyesével elindulunk a 2-től, és az n első osztóját keressük. Ilyen osztó biztosan lesz és ez biztosan prím. (Ez a tevékenység egy kiválasztás.) A soron következő prímosztó kereséséhez az előbb talált prímosztót ki kell valahogy venni az n számból. Ha elosztjuk vele az n-t, akkor a hányadosnak (az n új értékének) összes prímosztója az eredeti n számnak is prímosztói lesznek, és ezek éppen azok, amelyeket eddig még nem soroltunk fel explicit módon. A felsorolás addig tart, amíg az egyre csökkenő n nem lesz 1. Ez véges lépésben biztosan be fog következni.

Ezek alapján implementálhatjuk a felsorolás műveleteit. Egészítsük ki a felsoroló reprezentációját a legutoljára megtalált prímosztóval. A t felsorolót tehát két természetes szám reprezentálja: a fokozatosan csökkenő n szám és a d szám, amelyik a felsorolás alatt mindig az n legkisebb prímosztóját (lkpo(n)), tehát az eredeti n szám egy prímosztóját tartalmazza. Ezt a típus-invariánst kezdetben a First() művelettel biztosítjuk, amely kiválasztja az n szám legkisebb prímosztóját, ha n>1. (Ellenkező esetben nem kell tenni semmit, hiszen ilyenkor nincsenek prímosztók, tehát a felsorolás már véget is ért.) A Next() művelet a soron következő prímosztót keresi. Ehhez előbb elosztja az n-t a d-vel, majd a hányadosnak kiválasztja a legkisebb prímosztóját, ha n>1. A Current() művelet a d értékét adja vissza, az End() művelet pedig n=1 esetén igaz értéket ad.

t                              ~             n,d
                t.First()                 ~             d:=lkpo(n)
              t.Next()                 ~             n:=n/d;d:=lkpo(n)
                t.End()                 ~             n=1
                t.Current()           ~             d

db:=0
d:=lkpo(n)
n>1
	db := db + d
	n:=n/d
	d:=lkpo(n)

A d:=lkpo(n) részfeladatot egy olyan elágazás oldja meg, amely n>1 esetben megkeresi az n legkisebb 1-től különböző osztóját. Ez egyben prímosztó is lesz. Mivel n>1 esetben ilyen biztos van, ezért ez a részfeladat a kiválasztás tételére vezethető vissza. A kiválasztás általános programozási tételét itt úgy kell alkalmazni, hogy a b:E®L feltétel a b(d)= d|n lesz. A felsoroló az egész számokat járja be 2-től indítva, és leállásakor a felsorolást végző index megegyezik a kiválasztás eredményével.

d:=lkpo(n)
n>1
d:=2
Ø d\|n		SKIP
	d:=d+1

Gyakoriak az olyan feladatok, ahol egy programozási tételt kell alkalmazni úgy, hogy a megoldó program álljon le, ha egy bizonyos feltétel teljesül. Például ha egy tömbben azt vizsgáljuk, hogy van-e legalább három páros szám, akkor ez egy olyan számlálás, amelynek nem kell végig mennie a tömb összes elemén, ha a számolt eredmény eléri a hármat. Egy ilyen feladathoz arra a felsorolóra van szükség, amelyiknek csak az End() művelete különbözik a tömb nevezetes felsorolójától.

Hasonlóan könnyedén kezelhetők azok a feladatok, ahol a megszokotthoz képest fordított bejárásra van szükség, mert mondjuk egy tömb utolsó adott tulajdonságú elemét keressük.

Általában nehéz feladatnak számítanak azok, ahol egy gyűjtemény elemi értékeinek csoportjait kell feldolgozni. Például egy szöveges fájl leghosszabb szavát keressük. Ilyenkor a felsorolónak nem a karaktereket, hanem a szavak hosszait kell bejárnia. A First() és a Next() művelet megkeresi az első illetve következő szó elejét, ha van ilyen akkor a végét is, és kiszámolja a hosszát, a Current() pedig ezt a hosszt adja vissza. Az End() művelet akkor vált igazra, ha már nem találtunk több szót.

Egyedi felsorolót igényel az összefuttatásos feladatok (kollatálás) megoldása. Tekintsük az alábbi feladatot: Adott n darab egész számokat tartalmazó szekvenciális inputfájl, mindegyik egyértelmű és növekvően rendezett. Készítsünk olyan felsorolót, amely a fájlokban előforduló összes egész számot felsorolja úgy, hogy egy számot csak egyszer ad meg.

A felsorolót az összes előreolvasott szekvenciális inputfájllal reprezentáljuk. Ez három 1-től n-ig indexelhető tömbbel ábrázolható: f:infile(Z)ⁿ, df:Zⁿ , sf:Státuszⁿ, amely rendere az előre olvasott fájlokat, az előre olvasás során kinyert elemeket, és az olvasások státuszait tartalmazza. A kezdeti beolvasásokat a First() művelet végzi. Az End() művelet akkor ad igazat, ha mindegyik fájl olvasási státusza abnorm lesz. Ennek eldöntésére az 1..n intervallum feletti lineáris keresésre van szükség: vizsgáljuk, hogy "iÎ[1..n]:sf[i]=abnorm teljesül-e. A Current() művelet a soron következő egész számot az aktuálisan beolvasott egész számok közötti minimum-kereséssel határozza meg, de ki kell hagynia a vizsgálatból azon fájlokat, amelyek olvasási státusza már abnorm. Vegyük észre, hogy ez a feltételes minimum-keresés egyben az End() műveletet is implementálja, hiszen mellékesen eldönti, hogy van-e még nem üres fájl. Ezért tegyük bele ezt a First() (és később a Next()) művelet implementációjába), a felsoroló reprezentációjához pedig vegyük hozzá a minimum keresés eredményét tároló l logikai értéket, és min egész számot. Ekkor az End() értéke egyszerűen a Øl lesz, a Current() értéke pedig a min. A Next() műveletnek mindazon fájlokból kell új elemet olvasnia, amelyek aktuálisan kiolvasott értéke megegyezik a min értékkel, majd végre kell hajtania az előbb említett feltételes minimum-keresést.

*First()*
i=1..n
	sf[i],df[i],f[i]:read
l, min :=

*Next()*
i=1..n
	sf[i]=norm Ù df[i]=min
	sf[i],df[i],f[i]:read	SKIP
l, min :=

4.2. Implementáció

A felsorolóra megfogalmazott programozási tételek segítségével előállított algoritmusok kényelmesen implementálhatók az objektum orientált programozási nyelveken. Ennek oka az, hogy egy felsorolónak a típusát egy osztály segítségével könnyen leírhatjuk. Példaként nézzük meg egy kétirányú láncolt listával reprezentált kettős sorhoz rendelt felsoroló megvalósítását C++ nyelven:

class Sequence{

public:

enum Exceptions{EMPTYSEQ, UNDERTRAVERSAL};

private:

struct Node{

int val;

Node *next;

Node *prev;

Node(int c, Node *n, Node *p): val(c), next(n), prev(p){};

};

Node *first;

Node *last;

int iteratorCount;

public:

void Loext(int e);

int Lopop();

void Hiext(int e);

int Hipop();

friend class Iterator;

class Iterator{

public:

Iterator(Sequence *s):seq(s),current(NULL)

{++(seq->iteratorCount);}

~Iterator() {--(seq->iteratorCount);}

int Current()const {return current->val;}

void First() {current = seq->first;}

bool End() const {return current==NULL;}

void Next() {current = current->next;}

private:

Sequence *seq;

Node *current;

};

Iterator CreateIterator(){return Iterator(this);}

};

A visszavezetéssel született megoldásokat, ha azok nevezetes gyűjtemény nevezetes felsorolására épülnek, nagyon támaszkodhatunk a C++ nyelv STL könyvtárára. A szabványos tárolók (azaz a gyűjtemények) itt rendelkeznek egy begin() illetve egy end() metódussal, amelyek segítségével a tároló elemeinek bejárása megoldható. Az alábbi programrészletben a Collection egy szabványos tároló-sablon típusát jelöli, amelynek az elemeit (legyenek most egész számok) fel akarjuk sorolni, hogy alávessük azokat a void f(int) függvény tevékenységének, akkor az alábbi kódrészletre van szükségünk:[7]

Collection<int> v;

...

Collection<int>::iterator it = v.begin();

while(it!=v.end()){

f(*it);

++it;

}

Ugyanezt Java nyelven egy tetszőleges gyűjteményre és void f(Object) függvényre felírhatjuk. [8] Itt a felsoroló típusa Iterator, amely a hasNext() és a next() metódusokkal rendelkezik. Ezek megfelelnek az általunk bevezetett First(), Next(), Current() és End() műveleteknek.

Collection c = new Collection;

...

Iterator it = c.iterator();

while(it.hasNext()){

int current = (int)it.next();

f(current);

}

A C# nyelv a Java-hoz nagyon hasonló nyelvi elemeket biztosít. [9] Az IEnumerable típusú felsorolók az object Current(){get;}, a bool MoveNext() és a void Reset() metódusokkal rendelkeznek.

Collection c = new Collection();

...

IEnumerator it = c.GetEnumerator();

it.Reset();

while(it.MoveNext())

{

int current = (int)it.Current;

f(current)

}

A C# két olyan további nyelvi elemmel is rendelkezik, amely nagyon egyszerűvé teszi a felsorolók használatát és az egyedi felsorolók definiálását. A foreach ciklus segítségével anélkül alkalmazhatunk felsorolást (akár egyedi, akár nevezetes felsorolóval), hogy a felsoroló objektumot közvetlenül létre kellene hoznunk illetve annak metódusait közvetlenül meg kellene hívnunk. A fenti programrészlet így is írható, feltéve, hogy az f függvény nem változtatja meg a gyűjteményt.

Collection c = new Collection();

...

foreach(object o in c)

{

f(o);

}

Ha C# nyelven egyedi felsorolót akarunk készíteni, akkor azt egy IEnumerable interfészt megvalósító osztályban definiált GetEnumerator() metódus segítségével állíthatjuk elő. Ebben kellene példányosíani és visszaadni a felsorolót, de ez elkerülhető és a felsoroló IEnumerator-ból származtatott osztályát sem kell létrehoznunk, ha a megvalósításában a yield return utasítás segítségével megadjuk a felsoroló által bejárandó elemeket. Példaként álljon itt a „Határozzuk meg egy n pozitív egész szám prímosztóinak az összegét!” feladat megoldásának C# programrészlete.

class PrimDivisor : IEnumerable

{

static void Main(string[] args)

{

int sum = 0;

PrimDivisor pd = new PrimDivisor(int.Parse(Console.ReadLine()));

foreach (object d in pd)

{

sum += (int)d;

}

Console.WriteLine("A primosztók összege: {0} ", sum);

Console.ReadKey();

}

private int n;

private int d;

public PrimDivisor(int i)

{

n = i;

}

IEnumerator IEnumerable.GetEnumerator()

{

d = lkpo(n);

while (n != 1){

yield return d;

n = n / d;

d = lkpo(n);

}

int lkpo(int n)

{

if (n > 1){

d = 2;

while (n % d != 0) ++d;

}

return d;

}

Irodalom

1. Gregorics, T., Sike, S.:Generic algorithm patterns, Proceedings of Formal Methods in Computer Science Education FORMED 2008, Satellite workshop of ETAPS 2008, Budapest March 29, 2008, p. 141-150.

2. Andrei Alexandrescu, Herb Sutter: C++ kódolási szabályok. Kiskapu Kft. 2005.

3. Kent Beck: Implementációs minták. Panem 2008.

4. Csepregi, Sz., Dezső, A., Gregorics, T., Sike, S.: Automatic Implementation of Service Required by Components, PROVECS’2007 Workshop, ETH Technical Report 567. 2007.

5. Dijkstra E.W., A Discipline of Programming, Prentice-Hall, Englewood Cliffs, 1973.

6. Fóthi, Á.: Bevezetés a programozáshoz. ELTE-Eötvös Kiadó, 2005.

7. Stroustrup, B.: A C++ programozási nyelv, Kiskapu, 2001.

8. Angster, E.: Objektumorientált tervezés és programozás, 4KÖR Bt, 2004.

9. Sharp, J.: Visual C# 2005 lépésről lépésre, SZAK kiadó, 2005.

^{^[1]} Amikor a felsorolható adat egy gyűjtemény (iterált), akkor a felsoroló objektumot szokták bejárónak vagy iterátornak is nevezni, míg maga a felsorolható gyűjtemény a bejárható, azaz iterálható adat.

^{^[2]} A műveletek jelölésére az objektum orientált stílust használjuk: t.First() a t felsorolóra vonatkozó First() műveletet jelöli